Formula for Maximum Number of Segments Determined by N Points

I if Ai end max_nonoverlapping_segments. So we re create this table.

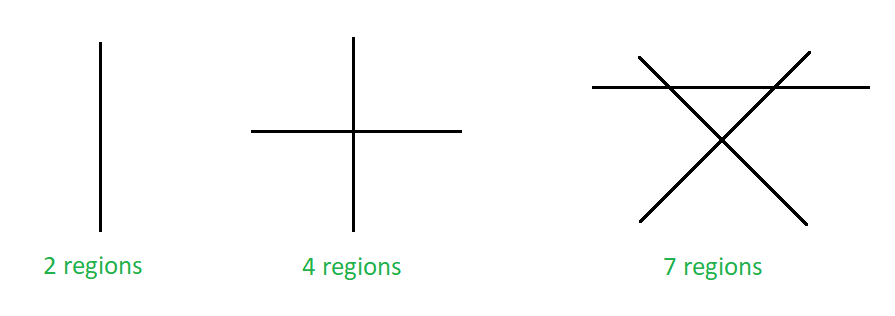
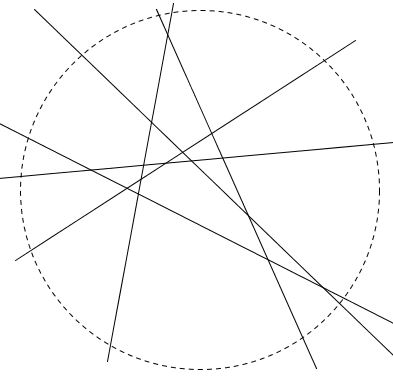
Maximum Number Of Region In Which N Non Parallel Lines Can Divide A Plane Geeksforgeeks

These two points up another segment in these two points as three segments we look at the top right point from here to this point is another segment from here.

. The numerator has two numbers. How to Find Number of Line Segments when points are given Rare Recreational Maths FormulaTrick avte maths formula. This problem can be thought of as a number of ways to select any two lines among n line.

Answer 1 of 5. The maximum number of point which lie on same line are 3 those points are 1 1 2 2 and 3 3 Example 2. If all faces are triangles then F 2 E 3 which gives us E 3 V 6.

The following steps would be useful to find the maximum and minimum value of a function using first and second derivatives. Let f x f x be a function. Now we can say that n u m s e g s 0 is 1 for segment 0 plus the maximum.

7 6 5 4 3 2 1 28The formula is P nn-12 which here is 8x72 28It. So we need to find the index of the first segment that is compatible with segment 0. Thus there are n 2 n n 1 2 possible lines.

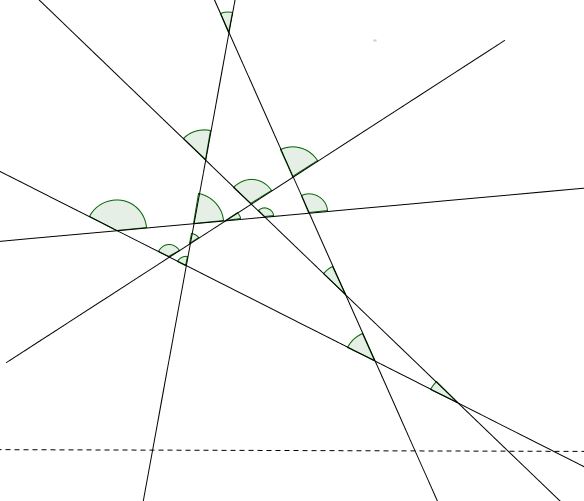
Define the set of intersection points mathcalP as those points p_k where drawn lines intersect each other we also include in mathcalP the. N n -1. Find the first derivative of f x which is f x.

Michal Forisek Apr 23 2009. If each of these edges was used only once to make a triangle the theoretical maximum number of triangles that can be created is the number of edges divided by three. A 1 1 2 2 1 2 3 3 2 3 Output.

The maximum number of electrons that an energy level can hold is determined from the formula 2n2 equals the total number where n is the energy level. That is why if the number on the left is n the one on the right is n - 1. The number on the right side of the multiplication is always 1 less the one on the left.

As every line intersects with others that are selected. N time with a simple binary search - let that index be k. Dp ib max dp i 1 dp ib.

Const int N Asize. Equate the first derivative f x to zero and solve for x which are called critical numbers. Arr 1 2 3 4 b 1 3 5 X 0 Y 0.

We can do this in O log. Dp ic max dp i 1 dp ic. Please try your approach on IDE first before moving on to the solution.

Below is the implementation of the above approach. So 2 can also be assigned to the first segment but it will not maximize the no. Int solutionvector.

Dp ia max dp i 1 dp ia. Given N point on a 2D plane as pair of x y coordinates Write a program to find the maximum number of point which lie on the same line. Assuming no three of the points are collinear which I think is a fair assumption for this question based on the answer any such line is uniquely determined by a choice of 2 of the n points.

Each added line n intersects n-1 other lines. So the total number of points nC2. Eulers formula for planar graphs states that in any planar simple graph with V vertices E edges and F faces we have V F E 2.

Conversely given any 2 points there is a unique line passing through them. Int max_nonoverlapping_segments 1. Into this point is another segment and lastly if we look at the bottom left negatives our last segment.

The 3 states to deal with are. After that iterate from 1 to n and for each of the 3 states ie dp ia dp ib and dp ic store the maximum value obtained by either using or not using the a b or c segment. Lets generalise to maximising the number of segments or regions for k lines dividing a rectangle.

What is the number of segments determined by. Given the task is to find the maximum of segments that can contain the given points. Given any N number of points the number of edgesline segments that can be formed is MATHN choose 2MATH.

Return max_nonoverlapping_segments. Below is the implementation of above idea. So the answer is 1.

So with four points the maximum number of segments is 123 or 56 six maximum number of segments. Hence for n 0 each maximum planar simple graph with n 2 vertices has 3 n edges. The denominator is always 2 so 2 will be the denominator in the general formula.

In this question we are looking for a pattern because we want to compare how the number of points compares with the maximum number of flying segments. From the given array a1 n1 line segments can be formed with starting and ending points as a1 i. For int i 1 end Bfront.

No points can be assigned to the second segment. Given an array a1 with size n1 and two integers A and B are given.

Number Of Regions N Lines Divide Plane

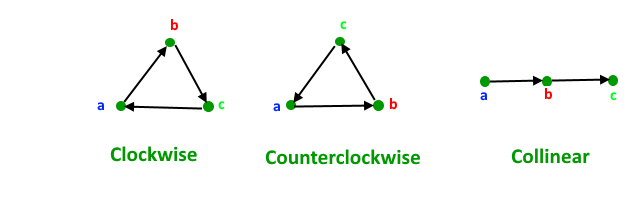
How To Check If Two Given Line Segments Intersect Geeksforgeeks

Number Of Segments Between Points

Number Of Regions N Lines Divide Plane